Background
The
Bridge Design Project primarily used West Point Bridge Design Software and
K’nex to show engineering students the basic concepts about how to build a
bridge and how the design affects its performance. West Point Bridge Design
helps students model, test, and optimize a steel highway bridge based on
realistic specification, constraints, and performance criteria. Below is the
link to a blog from a member of group 8 indicated their feeling of West Point
Bridge Design after using only a few time.
During the
process of learning how to interpret the data given by West Point Bridge
Design, some ideas of design had already been getting rid of because they could
not pass the truck test, see below.

Figure 1: A successful design in West Point Bridge Design
If a bridge
could not pass a simulated test how could that design and structure ever be
feasible enough to make a prototype. The designs which passed the test, needed
to improve because the high cost and inability of the K’nex pieces to be that
exact size or lay at that angle. Using the data gather from West Point Bridge
Design we could now start building plausible physical bridges out of K’nex.
K’nex behave more closely to a real
bridge than compared with West Point Bridge Design. It has to be built piece by
piece from nothing. There’s no sample bridge support be given like one West
Point Bridge Design. Thus, building a K’nex bridge a feasible idea and
blueprint is needed, a blueprint that could be found on a West Point Bridge
Design model that passed the truck test. West Point Bridge Design tests showed
that a bridge with top and bottom trusses is more stable than that only with
one side of truss, due to the more options the weight has to distribute. Thus
our initial, 24 inch K’nex bridge was born.
Figure 2: First design of K’nex bridge, 24” span
The
goal of this project is designing the most serviceable K’nex bridge by truss
analyzing. The ideal bridge would be loaded maximum loading with the lowest
cost after several forensic and static analyses.
Design Constraints
The
bridge span for the final design is a thirty-six inch minimum. The width of the
final design must be greater than three and a half inch. The bridge must be a
feasible prototype design to a real bridge, meaning that a scale car must be
able to fit through the bridge, the constraint for this was that a three inch
by two inch tube be able to fit continuously through the span of the bridge.
Design Process
The goal of our bridge is to design a most
severable bridge with the lowest cost. Our 24” inch bridge was mostly build using
the 1.125” inch chord. In the final bridge, the bridge size is increase, so we
use 3.375” long chord instead of the 1.25”one. By testing how different angles
work in the bridge. By the calculations we got the middle section is the part
which undergoes most of the tension, so we change the middle part to smaller
truss, so it can separate the tension of the loads. At the fist design we made
the end members very strong as they must negate the force and are under as much
force as the middle ones, so we get rid of some chord to short the cost. The
original design also had numerous non-fixed member connecting the two halves.
This was untimely the reason the first bridge failed, the non-fixed connection
allowed the bridge to twist and lean and cause the first bridge to fall over on
itself due to too much leaning
The double truss
structure was an idea taking from the individual bridge design portion of the
project. In the individual project one of designs was to have a single truss
structure bridge, the other was a double structure bridge. The data gather by
West Point Bridge designer showed that the double structure had a more stable
shape and only increase the cost by a minimal amount, thus giving us our basic
shape. Our final shape and size of the bridge is decided by testing physical
model and data obtained thought experimenting on the bridge designer website.
Using the data we gathered in latter we were able get the data we need and
improve the bridge without test our real bridge and having to go through
rigorous trial and error. This also helped avoid wearing down the pieces and
accidentally damage and weaken them avoiding possible unwanted failures but to
the condition of the pieces. Of course theory can only go so far so physical
test must be done as well. We did test our bridge use reams of paper (500 pages
of standard computer printer paper) and book. Upon weighting the books on a
scale we found our bridge could hold a load a bit above 30 pounds. It is a good
number base on the low cost of the bridge.
Final Design
The
final design was a top and bottom truss bridge, which used a fair number of
pieces, more than the bare minimum but far from excessive to keep the cost to a
minimal. The connection between the two halves was by fixed connection on the
top, middle, and bottom rows. It also had a few non fixed connections spanning
across the halves, this was done to save money and through testing was found
that having so few would not compromise the bridge strength and cause it to
possible twist or lean to one side when weight was added leading to a premature
failure. The idea behind the top and bottom truss is that the more connections
there are the more ways the weight’s force can travel, having both a top and
bottom mean that the main area the weight will be focused, that being the
center and central top have more options to escape to and the weight will be
distributed to the top and bottom and could be sent to the end in more options.
This design did work much better than just having a top or bottom truss in
testing thus it was chosen as the favorable shape.
Figure 3. Final Design in Final Test
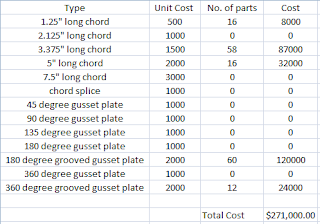
Below
is a table of the parts, number of the parts and the cost, with the total piece
count and cost at the bottom of their respective columns. Final piece count was
196 and the final cost was $307,000.
Table 1: Bill of
Material
Testing Results
The
load at failure of the final design was 17.0 pounds. The failure was around the
center area and towards the bottom of the bridge and was the result of two
grooved gussets being pulled apart as shown below. A very small and simple
failure that resulted in the bridge remaining whole and simply falling through
the span rather than violently being ripped apart and being almost completely
destroyed in failure. In terms of bridge failures this was a very calm and more
favorable break.
Figure 4. Failed Connection
Conclusion of Results
The
final test did not behave as predicted and did not behave like any of the
previous tests. In terms of the load the final design only held 17.0 pounds
where the final version of the twenty-four inch span held 34.0 pounds. The
final design only preformed half as well as the twenty-four inch span model
meaning the design did not improve but rather became worst. The predicted load
was forty pound, which was on the high side, thought multiple test on the final
design prior held an average of around thirty to thirty-five pound, in which forty
pound would not be too far off. This final test was most likely the fluke of
all the testing and may be due to how the bridge failed.
In
many of the prior test and the twenty-four inch span test failed very close to
the ends of the bridge due to all the surrounding members being pulled out of
the gussets and the center falling straight down, usually resulting in a clean
break leaving the bridge in two or three solid pieces and no single loss member
or gusset. In the final test however, the grooved gussets pulled apart from
each other around the center of the bridge, leaving it whole but with pieces
not fixed together. The image below shows where the bridge normally failed (in
blue) and where it failed in the last test (in red).
Figure 5. Usual Failed Connections and Final Test Failed Connections
The bridge only failed in
the center area and because of grooved gussets being pulled apart once during
all the prior testing. The conclusion as to why it failed like this is either
due to a missed defect prior to testing or some small difference in this test
that did not occur in the previous tests. Regardless, the final test did not
behave as the previous test had shown, but that is just how things work out and
so long as we can learn and understand from this failure there is always room
for improvement in the future.
Future Improvements
Given
the chance to modify our design to another version, the largest change would be
to build a bridge with only one truss. The two truss worked but when it counted
seemed to fail up to its standard and the extra pieces added a fair cost to the
bridge, making a one truss bridge would save money and that saved money could
be use to add extra support to critical areas such as the center and ends and
would allow for more cross connections between the two halve stabilize the
bridge, and we feel confident that a one truss bridge
could hold more than the final test did and even save money.